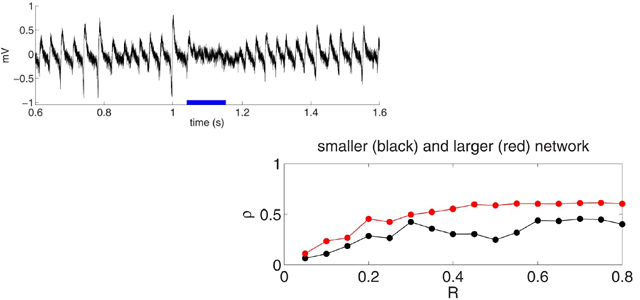
In networks of excitatory and inhibitory neurons with mutual synaptic coupling, specific drive to sub-ensembles of cells often
leads to gamma-frequency (25–100 Hz) oscillations. When the number of driven cells is too small, however, the synaptic
interactions may not be strong or homogeneous enough to support the mechanism underlying the rhythm. Using a combination of
computational simulation and mathematical analysis, we study the breakdown of gamma rhythms as the driven ensembles become too
small, or the synaptic interactions become too weak and heterogeneous. Heterogeneities in drives or synaptic strengths play an
important role in the breakdown of the rhythms; nonetheless, we find that the analysis of homogeneous networks yields insight
into the breakdown of rhythms in heterogeneous networks. In particular, if parameter values are such that in a homogeneous
network, it takes several gamma cycles to converge to synchrony, then in a similar, but realistically heterogeneous network,
synchrony breaks down altogether. This leads to the surprising conclusion that in a network with realistic heterogeneity, gamma
rhythms based on the interaction of excitatory and inhibitory cell populations must arise either rapidly, or not at all. For
given synaptic strengths and heterogeneities, there is a (soft) lower bound on the possible number of cells in an ensemble
oscillating at gamma frequency, based simply on the requirement that synaptic interactions between the two cell populations be
strong enough. This observation suggests explanations for recent experimental results concerning the modulation of gamma
oscillations in macaque primary visual cortex by varying spatial stimulus size or attention level, and for our own experimental
results, reported here, concerning the optogenetic modulation of gamma oscillations in kainate-activated hippocampal slices. We
make specific predictions about the behavior of pyramidal cells and fast-spiking interneurons in these experiments.